Event Generation Model
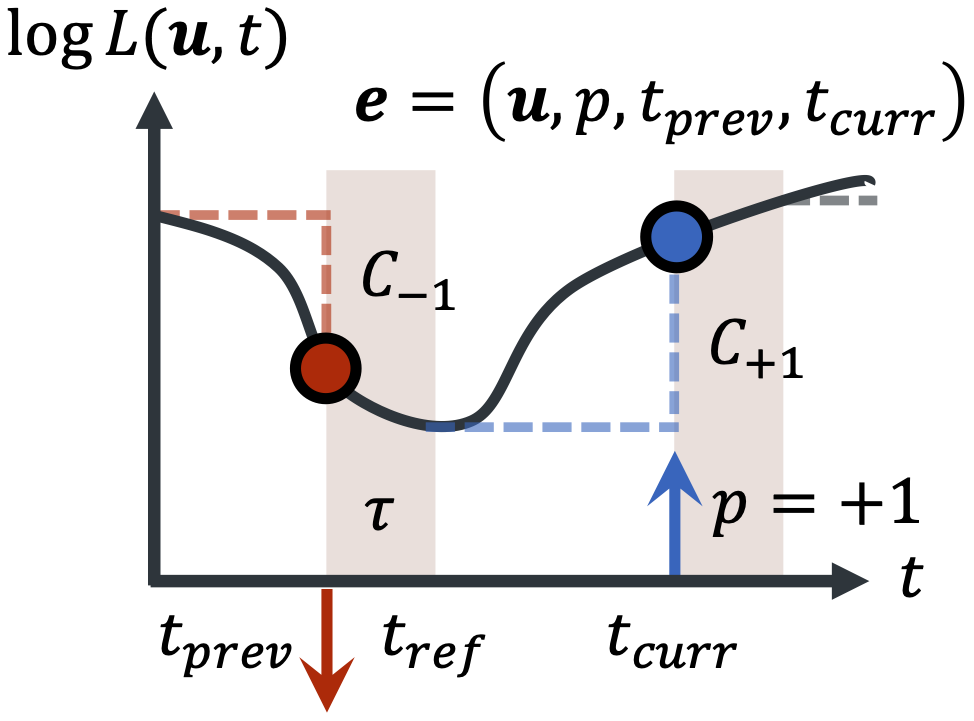
An event $\bm{e}$ of polarity $p$ is generated at timestamp $t_{\mathit{curr}}$ when the difference in log-radiance $\log L$ at a pixel $\bm{u}$, measured with respect to a reference $\log L$ at timestamp $t_{\mathit{ref}}$, has the same sign as $p$ and a magnitude that equals to the contrast threshold associated to polarity $p$, $C_p$. Red, downwards and blue, upwards arrows represent events of polarities $-1$ and $+1$, respectively, and each right-angled dashed line represents the measured change in $\log L$.
After an event is generated, the pixel will be temporarily deactivated for an amount of time given by the refractory period $\tau$, as shaded in the figure. Thus, $t_{\mathit{ref}}$ is simply the sum of the previous event timestamp $t_{\mathit{prev}}$ and $\tau$.
Training Pipeline
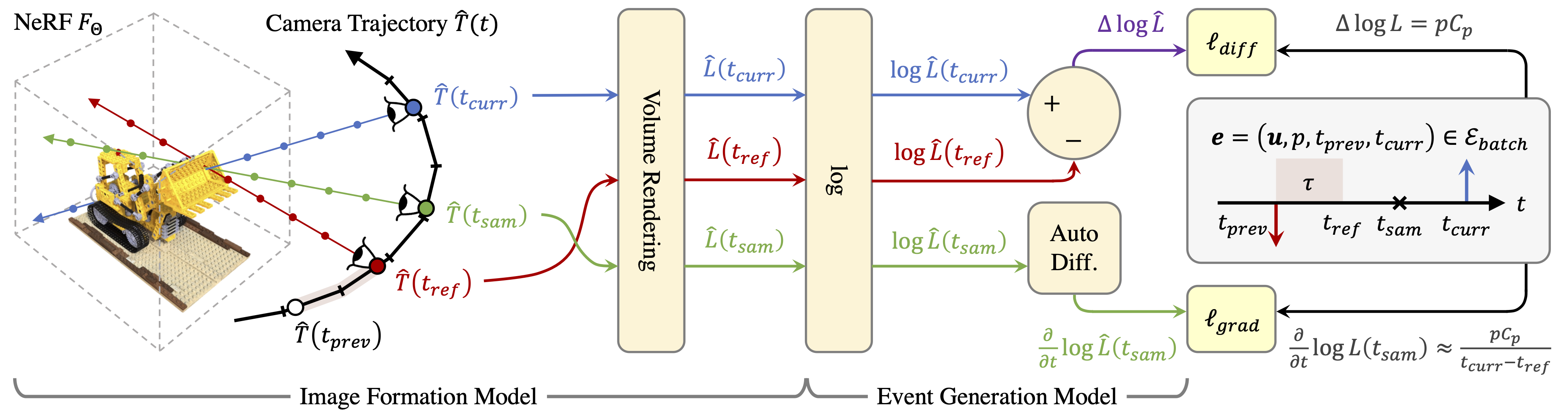
For each event $\bm{e}$ in the batch $\mathcal{E}_{\mathit{batch}}$ sampled randomly from the event stream, we first derive the reference timestamp $t_{\mathit{ref}}$, given the refractory period $\tau$, and sample a timestamp $t_{\mathit{sam}}$ between $t_{\mathit{ref}}$ and $t_{\mathit{curr}}$. Next, we interpolate the given constant-rate camera poses at $t_{\mathit{ref}}, t_{\mathit{sam}}$ and $t_{\mathit{curr}}$ using LERP for position and SLERP for orientation.
Given these pose estimates $\hat{T}$, we then perform volume rendering on the back-projected rays from pixel $\bm{u}$ with the NeRF $F_\Theta$. This is done to infer the predicted radiance $\hat{L}$, and thus log-radiance $\log{\hat{L}}$, of pixel $\bm{u}$ at $t_{\mathit{ref}}, t_{\mathit{sam}}$ and $t_{\mathit{curr}}$. For brevity, we denote $\hat{L} (t) = \hat{L} (\bm{u}, t)$.
These $\log{\hat{L}}$ are ultimately used to derive the predicted log-radiance difference $\Delta \log \hat{L}$ and gradient $\frac{\partial}{\partial t} \log \hat{L} (t_{\mathit{sam}})$ for the computation of the reconstruction loss: threshold-normalized difference loss $\ell_{\mathit{diff}}$ and smoothness loss: target-normalized gradient loss $\ell_{\mathit{grad}}$, given the observed log-radiance difference $\Delta \log L$ and gradient $\frac{\partial}{\partial t} \log L (t_{\mathit{sam}})$ approximation from the event $\bm{e}$, respectively.
Results
Overall

Dense and Noise-Free Events under Uniform Motion







Robust e-NeRF also better reconstructs fine details and preserves color accuracy, especially at the background.
Robustness to Temporal Event Sparsity
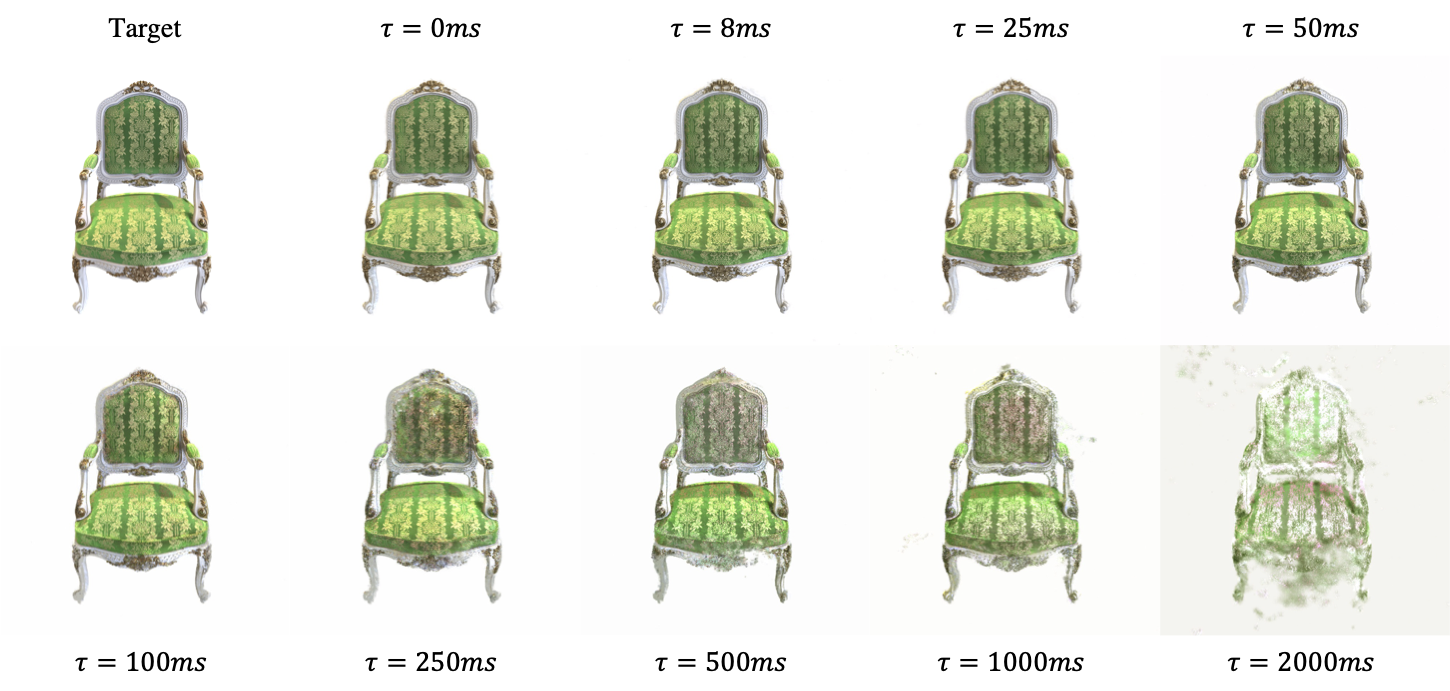
Robust e-NeRF demonstrates astonishing robustness under severely sparse event streams, which suggests its high data efficiency. Notably, reasonable accuracy can still be achieved with $\tau = 1000 \mathit{ms}$, where each pixel can only generate at most 4 events throughout the $4000\mathit{ms}$ sequence and the event stream is around $200 \times$ sparser than that of $\tau = 0 \mathit{ms}$.